Perform the Indicated Operations and Write the Result in Standard Form a+bi
College Algebra
Tutorial 12: Complex Numbers
![]() Learning Objectives
Learning Objectives
After completing this tutorial, you should be able to:
- Take the principle square root of a negative number.
- Write a complex number in standard form.
- Add and subtract complex numbers.
- Multiply complex numbers.
- Divide complex numbers.
![]() Introduction
Introduction
In this tutorial we will be looking at imaginary and complex numbers. Imaginary numbers allow us to take the square root of negative numbers. I will take you through adding, subtracting, multiplying and dividing complex numbers as well as finding the principle square root of negative numbers. I do believe that you are ready to get acquainted with imaginary and complex numbers.
![]() Tutorial
Tutorial
![]() where
where ![]()
This is the definition of an imaginary number.
From here on out, anytime that you have the square root of -1 you can simplify it as i and anytime you have![]() you can simplify it as -1.
you can simplify it as -1.
of
Complex Numbers
![]()
Complex numbers are made up of a real number part and an imaginary number part.
In this form, a is the real number part and b is the imaginary number part.
Note that either one of these parts can be 0.
An example of a complex number written in standard form is
![]() .
.
of
Complex Numbers
![]()
if and only if a = c AND b = d.
In other words, two complex numbers are equal to each other if their real numbers match AND their imaginary numbers match.
Complex Numbers
![]()
![]()
In other words, when you add or subtract two complex numbers together, you add or subtract the real number parts together, then add or subtract their imaginary parts together and write it as a complex number in standard form.
| | *Add the real num. together and the imaginary num. together |
| | *Subtract the real num. together and the imaginary num. together |
Complex Numbers
Step 1: Multiply the complex numbers in the same manner as polynomials.
Step 2: Simplify the expression.
Add real numbers together and imaginary numbers together.
Whenever you have an![]() , use the definition and replace it with -1.
, use the definition and replace it with -1.
Step 3: Write the final answer in standard form.
Step 1: Multiply the complex numbers in the same manner as polynomials
AND
Step 2: Simplify the expression.
| | *Use dist. prop. to multiply * i squared = -1 |
Step 3: Write the final answer in standard form.
| | *Complex num. in stand. form |
Step 1: Multiply the complex numbers in the same manner as polynomials
AND
Step 2: Simplify the expression.
| | *Use FOIL method to multiply *Combine imaginary numbers |
Step 3: Write the final answer in standard form.
| | *Complex num. in stand. form |
Complex Numbers
Step 1: Find the conjugate of the denominator.
You find the conjugate of a binomial by changing the sign that is between the two terms, but keep the same order of the terms.
a + bi and a - bi are conjugates of each other.
Step 2: Multiply the numerator and the denominator of the fraction by the conjugate found in Step 1.
Keep in mind that as long as you multiply the numerator and denominator by the exact same thing, the fractions will be equivalent.
When you multiply complex conjugates together you get:
![]()
Step 3: Simplify the expression.
Add real numbers together and imaginary numbers together.
Whenever you have an![]() , use the definition and replace it with -1.
, use the definition and replace it with -1.
Step 4: Write the final answer in standard form.
Step 1: Find the conjugate of the denominator.
In general the conjugate of a + bi is a - bi and vice versa.
So what would the conjugate of our denominator be?
It looks like the conjugate is![]() .
.
Step 2: Multiply the numerator and the denominator of the fraction by the conjugate found in Step 1
AND
Step 3: Simplify the expression.
| | *Multiply top and bottom by conj. of den. * |
Step 4: Write the final answer in standard form.
| | *Divide each term of num. by 5 *Complex num. in stand. form |
Step 1: Find the conjugate of the denominator.
In general the conjugate of a + bi is a - bi and vice versa.
So what would the conjugate of our denominator be?
It looks like the conjugate is![]() .
.
Step 2: Multiply the numerator and the denominator of the fraction by the conjugate found in Step 1
AND
Step 3: Simplify the expression.
| | *Multiply top and bottom by conj. of den. * |
Step 4: Write the final answer in standard form.
| | *Divide each term of num. by 29 *Complex num. in stand. form |
of a Negative Number
For any positive real number b, the principal square root of the negative number, -b, is defined by
![]()
| | *Principal square root of -100 *Complex num. in stand. form (note real num. part is 0) |
negative numbers.
In other words use the definition of principal square roots of negative numbers before performing any operations.
Step 2: Perform the indicated operation.
Step 3: Write the final answer in standard form.
| | *Square root of a negative is i |
Step 2: Perform the indicated operation
AND
Step 3: Write the final answer in standard form.
| | *The square root of 4 is 2 |
| | *Square root of a negative is i |
Step 2: Perform the indicated operation
AND
Step 3: Write the final answer in standard form.
| | *Square root of a negative is i |
Step 2: Perform the indicated operation
AND
Step 3: Write the final answer in standard form.
| | *The square root of 25 is 5 *Divide each term of num. by 5 *Complex num. in stand. form |
| | *Square root of a negative is i |
Step 2: Perform the indicated operation
AND
Step 3: Write the final answer in standard form.
| | * i squared = -1 |
![]() Practice Problems
Practice Problems
These are practice problems to help bring you to the next level. It will allow you to check and see if you have an understanding of these types of problems. Math works just like anything else, if you want to get good at it, then you need to practice it. Even the best athletes and musicians had help along the way and lots of practice, practice, practice, to get good at their sport or instrument. In fact there is no such thing as too much practice.
To get the most out of these, you should work the problem out on your own and then check your answer by clicking on the link for the answer/discussion for that problem. At the link you will find the answer as well as any steps that went into finding that answer.
Practice Problems 1a - 1i: Perform the indicated operation. Write the answer in standard form.
![]() Need Extra Help on these Topics?
Need Extra Help on these Topics?
![]()
Videos at this site were created and produced by Kim Seward and Virginia Williams Trice.
Last revised on Dec. 15, 2009 by Kim Seward.
All contents copyright (C) 2002 - 2010, WTAMU and Kim Seward. All rights reserved.
Perform the Indicated Operations and Write the Result in Standard Form a+bi
Source: https://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut12_complexnum.htm
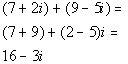
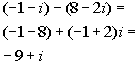
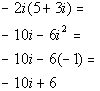
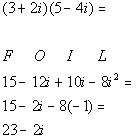
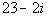
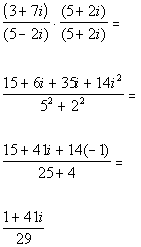
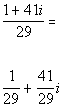
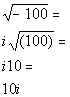
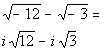
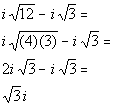
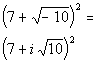
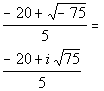
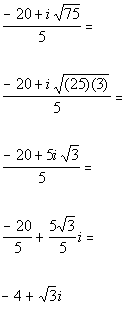
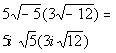
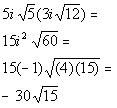
Yorum Gönder for "Perform the Indicated Operations and Write the Result in Standard Form a+bi"